|
直接數字頻率合成(DDS)是近年來得到迅速發展的一種新的頻率合成方法,具有頻率切換速度快,很容易提高頻率分辨率、對硬件要求低等優點。可編程全數字化便于單片集成、有利于降低成本、提高可靠性并便于生產等有點。DDS技術從相位的概念出發進行頻率合成,存儲了數字采樣波形表,可以產生點頻、線性調頻、ASK、FSK等各種形式的信號。線性調頻信號可以獲得較大的壓縮比,有著良好的距離分辨率和徑向速度分辨率,作為一種常用的脈沖壓縮信號,已經廣泛應用于高分辨率雷達領域。 Matlab是美國MathWorks公司自20世紀80年代中期推出的數學軟件,優秀的數值計算與卓越的數據可視化能力使其很快在同類軟件中脫穎而出。Matlab已經發展成為多學科、多種工作平臺的功能強大的大型軟件。本文用Matlab軟件建立DDS系統中線性調頻信號的仿真模型,對于理解線性調頻信號和在FPGA中來實現線性調頻信號有借鑒意義。 DDS線性調頻信號發生器框圖設計 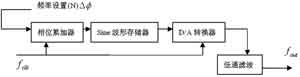 圖 1 DDS技術的基本原理 1 DDS技術的基本原理 基本模型如圖1所示,主要由時鐘頻率源fclk、相位累加器、波形存儲器(ROM)、數/模轉換器(D/A)、以及低通濾波器(LPF)組成。輸出信號波形的頻率表達式為: (1)式中,fclk為參考時鐘頻率,ΔΦ為相位增量,N為相位累加器的位數。只要N足夠大,DDS可以得到很小的頻率間隔。要改變DDS的輸出信號的頻率,只要改變ΔΦ即可。當參考時鐘頻率給定后,輸出信號的頻率取決于頻率的控制字,頻率分辨率取決于累加器的位數,相位分辨率取決于ROM的地址位數,幅度量化取決于ROM的數據字長和D/A轉換器的位數。 2 線性調頻信號的實現框圖 圖2 軟件編程實現線性調頻信號的原理圖 脈沖壓縮雷達最常見的調制信號是線性調頻信號,接收時采用匹配濾波器(Matched Filter)壓縮脈沖。它的數學表達式如下: 式中fe為載波頻率,K=B/T是調頻斜率,于是,信號的瞬時頻率為。 其對應的量化公式如下(此式是以圖2實現的原理公式): 式中N為相位累加器的位數,Kc為頻率控制字,K為上式中的調頻斜率。 圖1所示的DDS原理框圖是用于實現固定頻率的正弦波信號,按照公式(3)的思路實時改變ΔΦ,即可產生線性調頻信號。 經過頻率累加器輸出的是嚴格線性增長的瞬時頻率。在實際過程中,相位累加器的輸出是經過相位截斷再進行尋址,從而引入了一定的相位誤差,雖然這一誤差會影響到線性調頻信號的線性度,但是調頻斜率為相位的二次導數,相位截斷誤差本身已很小,所以對調頻線性度的影響就更小了。在本文的Matlab實現中暫時不考慮截斷問題,忽略不計。 3 Matlab軟件建模實現線性調頻信號 本程序遵照上述軟件編程實現線性調頻信號的原理圖編寫,采用.m文件的方式編寫,下面是實現的源程序: %調頻信號的累加器實現 clear all;clc %清除所有變量,清屏 M=2^11; %采樣的點數 a(1:1:M)=0; %頻率累加器的數值 b(1:1:M)=0; %相位累加器的數值 y(1:1:M)=0; %輸出的波形數據 K=400; %調頻斜率 Kc=10; %初始頻率控制字 N=10; %幅度量化位數 L=24; %相位累加器位數 %下面一段實現頻率累加器 a(1)=0.5*K; %初始頻率步進量 for i=2:1:M a(i)=a(i-1)+K; end %下面一段實現相位累加器 b(1)=Kc+a(1); %相位初始值 for i=2:1:M b(i)=b(i-1)+(Kc+a(i)); end %下面一段實現了查找表ROM以及進行幅度量化 for i=1:1:M y(i)=floor(2^N*cos(2*pi/(2^L)*b(i))); end %下面一段畫出相應的圖形 figure(1);plot(y);axis([0 M,-2^N-100 2^N+100]); figure(2);freqz(y) 上面這段程序中,有很多的變量,包括調頻斜率K、頻率控制字Kc、幅度量化位數N以及相位累加器位數L等等,修改不同變量值可以得到各,不同的線性調頻信號。具體的實現要根據實際的需要來設置。 4 實驗結果 根據上面的程序,取調頻斜率為400,頻率控制字為10,幅度量化為10位(和所使用的D/A配合),相位累加器為24位,用Matlab仿真得到的線性調頻信號的波形和相應的幅頻響應如圖3和圖4所示。 圖3 K=400,Kc=10,N=10,L=24的情況下的線性調頻信號 圖4 針對圖3的幅頻特性曲線 結束語 本文所講的線性調頻信號的產生原理和方法有很好的可擴展性,修改頻率累加器的內容即可以實現其他的各種調頻信號。作為線性調頻信號,由于廣泛應用于高分辨率的雷達系統中,因此正確理解線性調頻信號的產生原理和掌握其產生的方法是很有現實意義的。在實際應用中主要采用專用DDS芯片或者FPGA來實現線性調頻信號(各有優缺點),而本文則基于Matlab軟件的良好編程性來驗證這一方案,仿真結果較好的證明本方案的可行性,完成了預期的方案設計和論證。 |